1月11日
皆さん、かなり遅れてしまいましたが、あけましておめでとうございます!
...というわけで、やっぱり2025年は新年らしいテーマで始めようと思います。
desmosで今年の干支、ヘビをつくりました。去年の龍よりは形が単純なので式自体少ない(言い訳)のですが...。
まあなので、今年は去年と違って『2025』の文字も足しました。
今回は二つ、こだわった部分を紹介していきたいと思います。
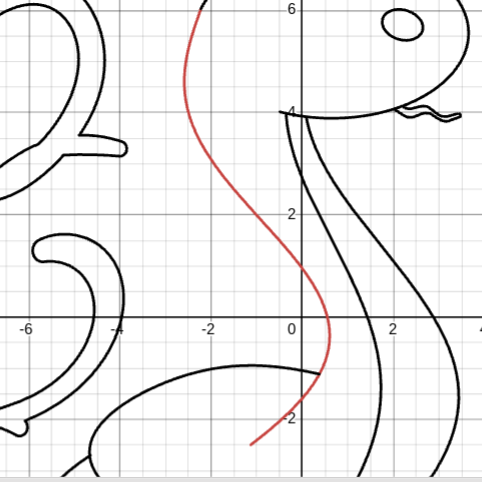
まず、上の写真の赤い部分です。これは媒介変数で作られています。
$$\left(\frac{t}{1.5}\sin\frac{t}{1.5}-2.5-0.4t,1.3t+4\right)$$
tの変域は除いていますが上の式で作られています。
媒介変数の説明は割愛しますが、曲線の表し方の一つですね。
媒介変数、初めて使ったといっても過言じゃないです(なので、なんとなく無駄がありそう(勘)な式になってしまいましたが...)。まともに媒介変数のことを知ったのは去年なので、今回はじめて媒介変数の技術を取り入れられたと思います。
媒介変数は便利なので、もっと使いこなして応用が効くようにしていきたいです。これは正直言って媒介変数を使わなくてもできた曲線なので。
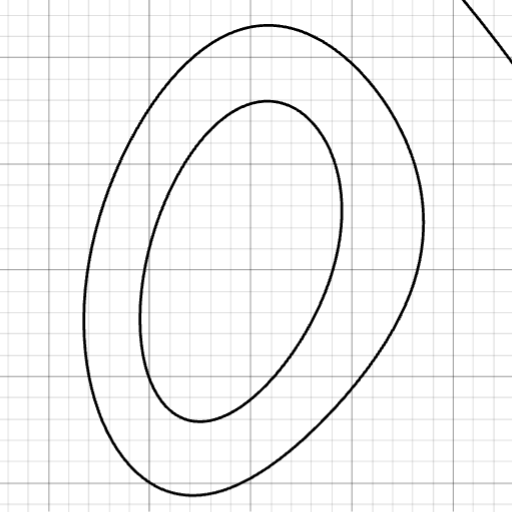
次に、この0です。普通の楕円でつくってもよかったんですが、ちょっと歪ませています。
普通の円は、
$$x^{2}+y^{2}=1$$
という式で表されますが、例えば
$$(x+siny)^{2}+y^{2}=1$$
というふうにしてみると、ちょっと円が歪んだりします。こんな感じでうまく楕円にして、回転行列を使って回転させて、移動させて、こんな感じの0が作れました。よく使われる歪ませ方(多分)ですが、この方法は他のところにも使っているので見てみてほしいです。例えばヘビの下らへんとか...。
この二つ以外にも、サインカーブを回転させたり、こだわりが色々あるので、数式を漁ってみてほしいです。
来年は午ですね。もっといろいろな技術を取り入れて作れるようにしていきたいです。
では、今年も一年張り切って!楽しく過ごしていきましょう!

