4月5日

みなさんこんにちは。新年度が始まりましたが、なにか今年度の目標だったりはありますか？

今回は前回の続きで、ゼータ関数に関する話題です。

3月22日のブログ

先週は『ゼータ関数に-1という数をいれると自然数の和が-1/12に収束してしまう。こんなおかしなことが起こったのはゼータ関数の定義域をはみ出してしまったから。』ということを書きました。

では、なぜ、それでも自然数の和は-1/12だと『主張することができる』のか？

それは解析接続というやり方と直結してきます。

解析接続とは...？

　

解析接続･･･要するに関数の定義域を広げる方法

　

次のような関数があるとします。

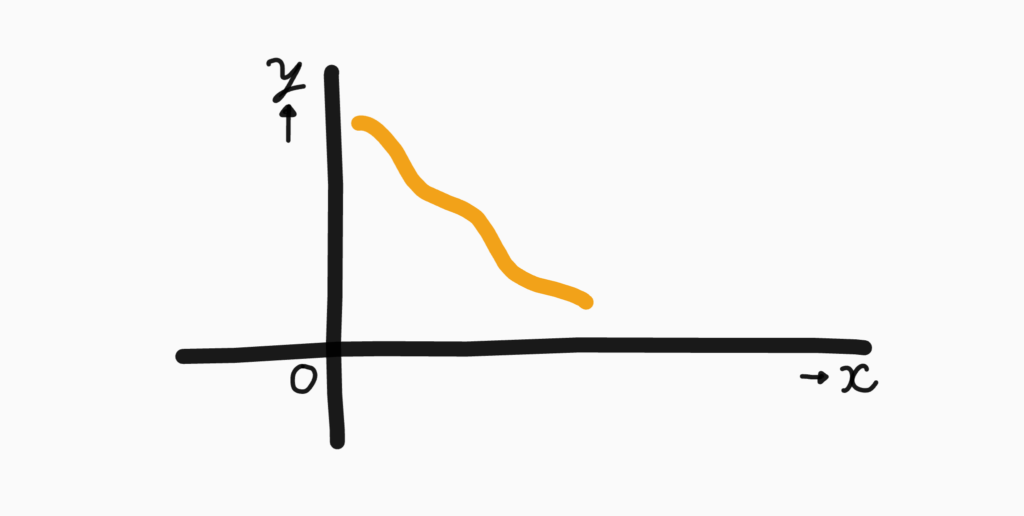
定義域が途中までしかありません。x軸が負の部分（y軸もですが）がありませんね。

かなり雑に説明するのですが、x=1の場合のyの値を求めたい。と思ってしまったらどうしましょう？

定義されていたいのでどうにもならないのですが、『無理やり』定義することはできます。

どうやって？答えは簡単。無理やり定義するんです。

この場合はどうすればいいか。例えば次のようにしたらちょうどいいと思いません？

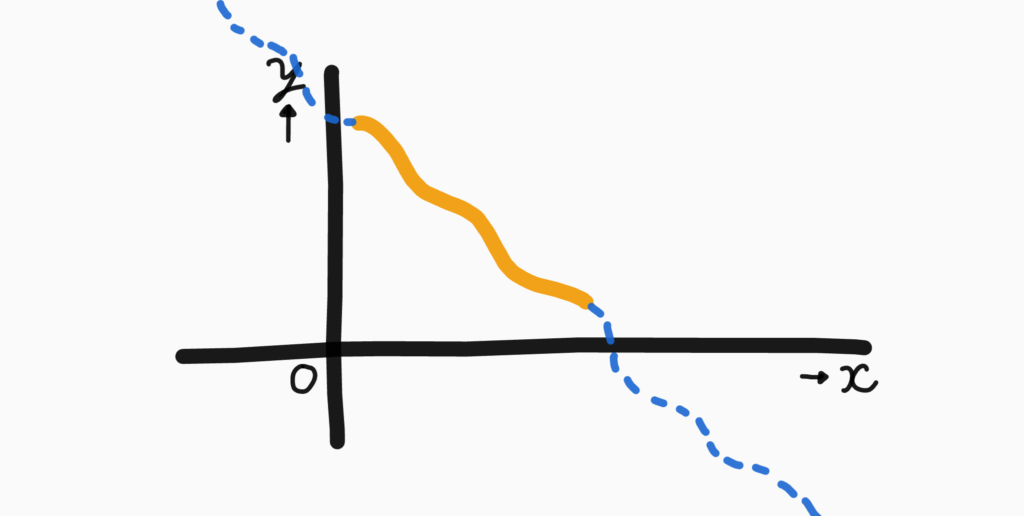
実はこの平面で「とある条件を満たして」滑らかに線を伸ばしていくことはそこまで難しくないのですが、「複素関数」というものを考えるとこの延長の仕方は一通りしかないということが示せるのです（一致の定理）。

ここではそのとある条件だの一致の定理だのについては割愛しますし、僕自身ちゃんと勉強したわけでもないのでもしかしたら解釈が間違っているかもしれませんので、参考程度にお願いします。

ただ、です。とにかくこの解析接続を使えば、関数の定義域を広げることができるのです。

　

さて、話をゼータ関数に戻します。

$$\zeta(x)=\sum_{n=1}^{\infty}\frac{1}{n^{x}}(x>1)$$

これはxが1より大きくないと定義されませんでしたが、解析接続を使うとxがそれ以外の場合も、ましてやxが負の場合も考えることが一応できます。

そして、導き出せるのが以下の公式というわけです。

$$1+2+\cdots+\infty=-\frac{1}{12}$$

誰かがこう主張するのも無理はないわけです。ただ何度も言いますが、間違ってはいます。間違っていますが、考えることもできるっていうだけです。

　

　

また、実は、これを使えば

$$\zeta(負の偶数)=0$$

というのも示せるそうです。

...何が言いたいか？

まずこの記事の趣旨としては、

$$\sum_{k=1}^{\infty}k^2$$

という和を考えることでした。...$\zeta(-2)$。少し計算するとわかるように、ゼータ関数が-2という数を取ると、それはこの平方数の和になります。

-2は負の偶数。つまり、

$$\sum_{k=1}^{\infty}k^2=0$$

といことがわかるのです！

不思議ですよね。自然数の和と同じように間違っていますが、結局ゼロになってしまうわけですね。また、負の偶数なら何でもいいので、

$$\sum_{k=1}^{\infty}k^4=0$$

ですし、

$$\sum_{k=1}^{\infty}k^{100}=0$$

なわけです。どれほど指数が大きくなってもいいなんて、...やっぱり不思議ですね。

　

今回と前回は平方数の和に関する話題でした。

解析接続。そしてゼータ関数との関係。無限に計算するということの面白さというのがわかります。感覚だけじゃわからない部分ってやっぱりあるんですね。

そしてゼータ関数はリーマン予想という数学の難問とも関係あります。興味のある方は調べてみてはいかがでしょうか。

では来週も一週間頑張りましょう！