7月5日
みなさんこんにちは。2025年も上半期が終わりましたね。
今回はパンデジタル数について紹介します。
パンデジタル数とは、しっかりいうと『n進法の自然数においてすべての位を見たときに0からn-1までの数が1つ以上含まれているもののこと』です。
普通に数としていつも使っているのは10進法ですが、10進法の場合は『すべての位を見たときに0から9の数がすべて含まれている自然数』ですね。ようするに1023456とか9728560431のことです。
また、例えば2進法なら、大抵の自然数はパンデジタル数になります。なぜなら0と1が現れていればいいからです。00000・・・と続くのはすべて0ですし、そもそも自然数ではありません。また11111・・・と続く自然数も限られてきます。75は二進数だと1001011なのでパンデジタル数になりますね。また、三進数でも2210と表せるのでパンデジタル数です。
また、75という数は、4進数においてきれいなパンデジタル数になります。1023と表せます。
要するに、75が4進数までならすべてパンデジタル数になるわけですね。また4進数なら最小のパンデジタル数は1023だとわかります。
さて、今回はパンデジタル数の中でもそれぞれの数が1回ずつだけ現れるものをきれいなパンデジタル数と呼びたいと思います。こんな問題を考えました。
n進法で$n^n-1$までの自然数をランダムに選んだ場合、それがきれいなパンデジタル数になる確率は?
n進法で$n^n-1$までの自然数というのは例えば10進法なら10桁までという意味です。
簡単な確率問題ですね。
ランダムに選ぶ自然数が何通りあるかは簡単に出ます。ある位で現れうる数(0含む)はn進数なのでn個あります。なので$n^n$となり、0の場合を除いて$n^n-1$通りとなります。この場合、最初に0が来てしまっても、例えば0123なら3桁の数として認識できるので大丈夫です。
きれいなパンデジタル数が何通りあるかも考えます。ある位には0からn-1のどれかが必ず入るので順列の問題ですね。単純に考えるとn種類あるので$n!$となりますが、この場合は最初に0が来る可能性を省かなければいけません。最初に0が来るとパンデジタル数にならないので。
最初に0が来るのが何通りかはそれ以降の位を考えればわかります。1からn-1までの数が入るので、$(n-1)!$ですね。
引き算して、$n!-(n-1)!$となります。変形すれば$(n-1)!(n-1)$ですね。
さて、分母と分子がでました。確率を計算はこうなります。
$$\frac{(n-1)!(n-1)}{n^n-1}$$
これをdesmosに入れてみました。
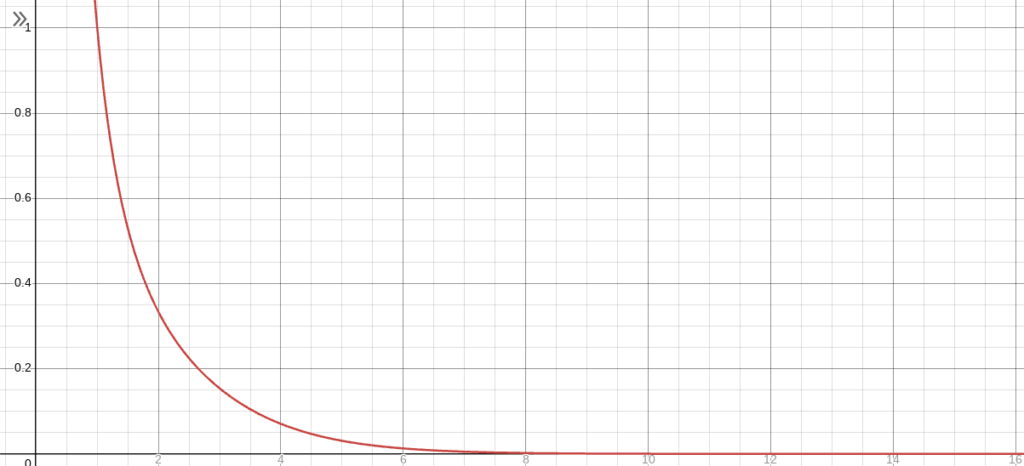
横軸がn進数のnを表していて、縦軸が確率です。縦軸と横軸で数が違うことに注意してください。
そもそも、分母がn進法で$n^n-1$までの自然数であり、n桁のものと限定していないため、かなり確率が低くなることはよくわかります。実際、10進数だと確率は0.03%くらいでした。
1進数で確率が100%になるのは当たり前ですよね。
今回はパンデジタル数について紹介しました。0から9までを使って一番小さい数をつくるみたいなことを小学校で習ったのを思い出します。
ではまたいい一週間を〜

